
Kedua tangga di atas memiliki ketinggian yang sama, akan tetapi lebarnya berbeda. Tangga biru memiliki lebar yang lebih kecil daripada tangga kuning. Apabila kamu disuruh untuk menaiki salah satu tangga tersebut, tangga manakah yang akan kamu naiki? Mungkin jawaban dari pertanyaan ini berbeda-beda. Apabila kita ingin cepat mencapai puncak, tentunya kita akan memilih tangga yang berwarna biru. Sedangkan apabila kita ingin menghemat tenaga kita, tentunya kita akan memilih tangga yang berwarna orange.
Dari kedua tangga di atas, kemiringan adalah hal yang membedakannya. Tangga biru memiliki kemiringan yang lebih besar (lebih tegak) daripada tangga kuning. Begitu juga dengan tangga, ruas garis pada bidang koordinat juga memiliki kemiringan tertentu. Perhatikan contoh 3 ruas garis berikut.
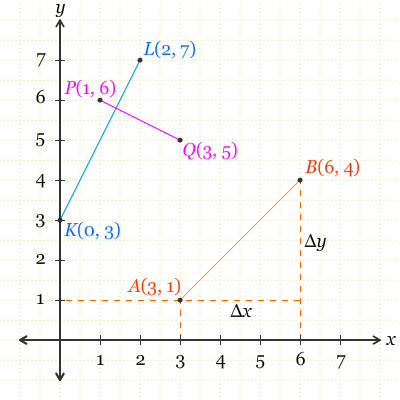
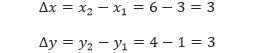
Kemiringan ruas garis AB dapat ditentukan dengan membagi Δy dengan Δx. Sehingga kemiringan ruas garis AB: Δy/Δx = 3/3 = 1. Kemiringan dari ruas garis ini selanjutnya disebut gradien.
Dari kesimpulan tersebut, kita juga dapat menentukan gradien dari ruas garis KL dan PQ. Gradien dari ruas garis KL adalah Δy/Δx = (7 – 3)/(2 – 0) = 4/2 = 2. Sedangkan gradien dari ruas garis PQ adalah (5 – 6)/(3 – 1) = –1/2.Gradien merupakan tingkat kemiringan ruas garis atapun garis. Gradien dapat ditentukan dengan membagi Δy dengan Δx.
Setelah mengetahui gradien pada ruas garis yag melalui dua titik tertentu, sekarang mari kita lanjutkan pembahasan kita mengenai gradien pada garis yang memiliki persamaan tertentu.
Menghitung Gradien pada Persamaan Garis y = mx
Garis yang memiliki persamaan y = mx melalui titik asal, O(0, 0). Karena apabila kita substitusikan x = 0, maka kita dapatkan y = m(0) = 0. Untuk (x, y) titik selain (0, 0) yang dilewati oleh garis y = mx, kita dapat menentukan gradien garis tersebut sebagai berikut.
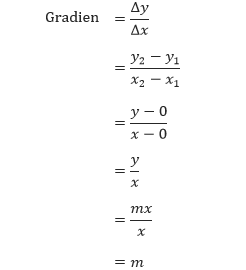
Perhitungan di atas dapat membawa kita untuk mengetahui gradien dari y = mx. Apa yang dapat kita peroleh dari perhitungan di atas?
Sebagai contoh kita dapat menentukan gradien dari garis yang memiliki persamaan y = 3x dan –2x = 5y. Dengan jelas kita dapat menentukan gradien dari y = 3x adalah 3. Bagaimana dengan gradien garis –2x = 5y? Untuk menentukan gradien garis tersebut, kita ubah dulu persamaan garis tersebut menjadi bentuk y = mx.Gradien dari garis yang memiliki persamaan y = mx adalah m.
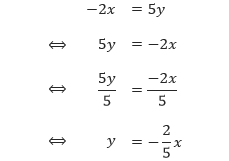
Dari perhitungan tersebut kita dapat memperoleh bahwa gradien dari garis –2x = 5y adalah –2/5.
Menghitung Gradien pada Persamaan Garis y = mx + c dan ax + by + c = 0
Misalkan dua titik K(x1, y1) dan L(x2, y2) dilalui oleh garis y = mx + c. Maka y1 = mx1 + c dan y2 = mx2 + c. Sehingga gradien dari garis y = mx dapat ditentukan sebagai berikut.
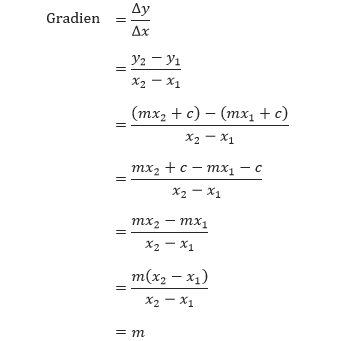
Sehingga gradien garis yang memiliki persamaan garis y = mx + c adalah m, yaitu koefisien dari x. Bagaimana dengan gradien dari garis yang memiliki persamaan garis ax + by + c = 0?
Untuk menentukan gradien dari ax + by + c = 0, kita ubah dulu persamaan ax + by + c = 0 menjadi bentuk y = mx + c, seperti berikut.
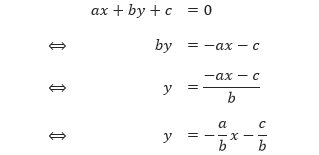
Dari uraian di atas, ax + by + c = 0 dapat diubah menjadi y = –a/b x – c/b. Sehingga, gradien dari ax + by + c = 0 adalah –a/b.
Dari kesimpulan di atas, kita dapat menentukan gradien dari garis y = 2x – 5 dan 3x – 2y – c = 0. Gradien dari garis y = 2x – 5 adalah 2, sedangkan gradien dari 3x – 2y – c = 0 adalah –(3/–2) = 3/2. Untuk lebih memahami mengenai gradien suatu garis, perhatikan contoh berikut.Gradien dari garis y = mx + c adalah m, sedangkan gradien dari garis ax + by + c = 0 adalah –a/b.
Contoh Soal
Berikut ini merupakan segitiga ABC.
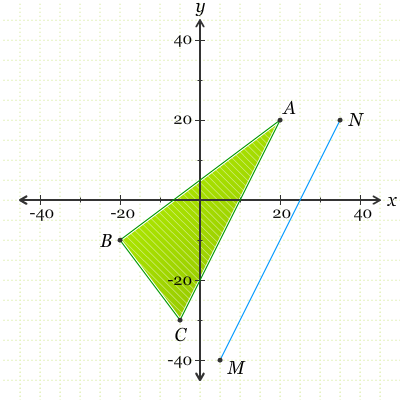
Tentukanlah gradien dari ruas garis AB, BC, AC, dan MN, kemudian tentukan pasangan ruas garis yang sejajar dan tegak lurus!
No comments:
Post a Comment